



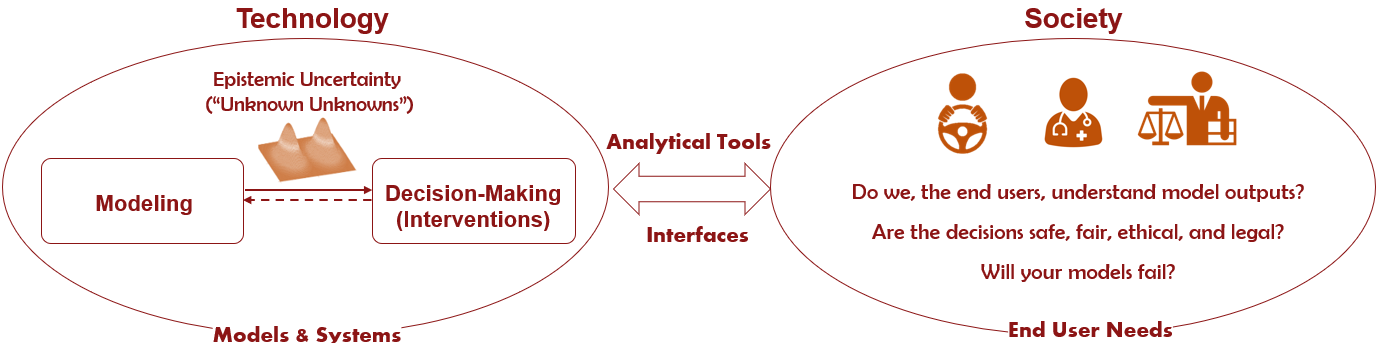
Machine learning (ML) has already made significant progress in modeling the world around us by, for instance, detecting physical objects and understanding natural language. Following these developments, we are now attempting to use ML to make decisions for us in application areas such as robotics. However, when we try to integrate these black-box ML models in such high-stakes physical systems, doubts among end users can arise: can we trust the decisions made by autonomous systems without understanding them? Or, can we even fix these systems when they behave in unintended ways, or design legal guidelines if we do not understand how they work? The focus of my research is to make learning-based robotics and automation explainable to end users, engineers, and legislative bodies alike. I develop tools and techniques at three different stages of automation to address the following questions.

Autonomous cars fail in adverse weather. The perception modules of an autonomous car uses more complex deep learning models compared to the control modules. Therefore, the perception modules are more susceptible to failures. Due to this complexity, exhaustively finding all failure modes is not practically possible. Hence, we formulate a method to find most likely failure modes. To this end, we construct a reward function in such a way that encourages the probabilistic likelihood of finding failures and uses reinforcement learning to explore those failures.
What happens if we deploy our model in a domain that it has never seen? For instance, if you train an object detection neural network based on data collected in the US and deploy it in Australia, what would the neural network do when it sees a kangaroo? Or, if we develop a mobil app for skin cancer detection, how will different light conditions and skin colors affect the results? We need ways to characterize these effects before we deploy a neural network in the real-world.

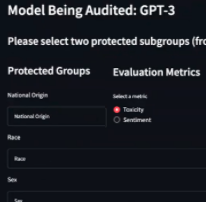
Large languge models trained on data scraped from the internet can exhibit undesirable behavior such as discrimination. In this work, we develop an interactive AI auditing tool to evaluate discrimination of such models in a human-in-the-loop fashion. Given the task of generating reviews from a few words, we can evaluate how much of toxicity the model exhibits against gender, race, etc. The tool outputs a summary report.
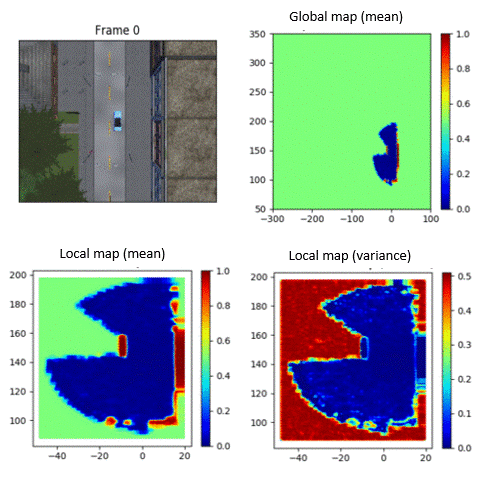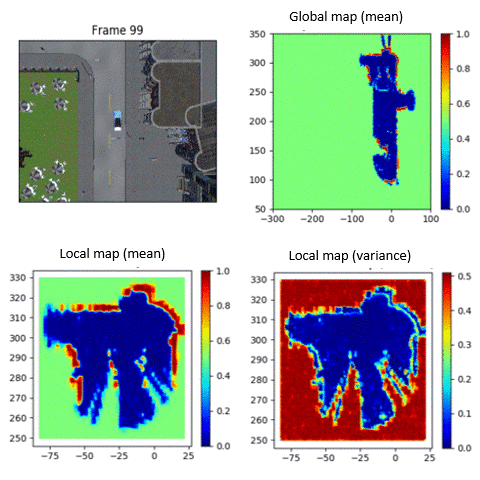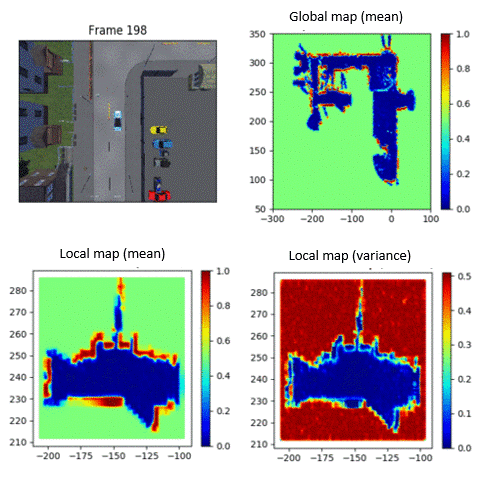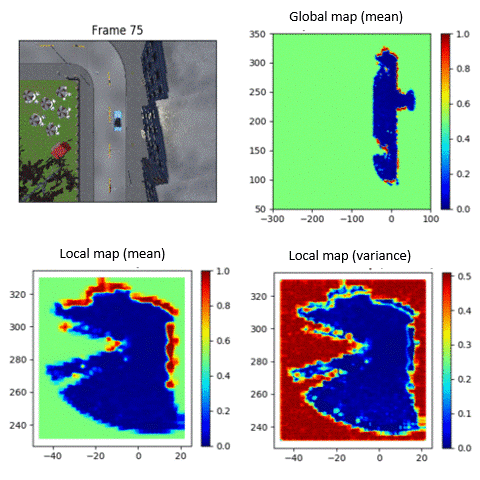
Modeling the uncertainty of occupancy of an environment is important for operating mobile robots. I have developed scalable continuous occupancy maps that can quantify the epistemic uncertainty in both static and dynamic environments. Summary:
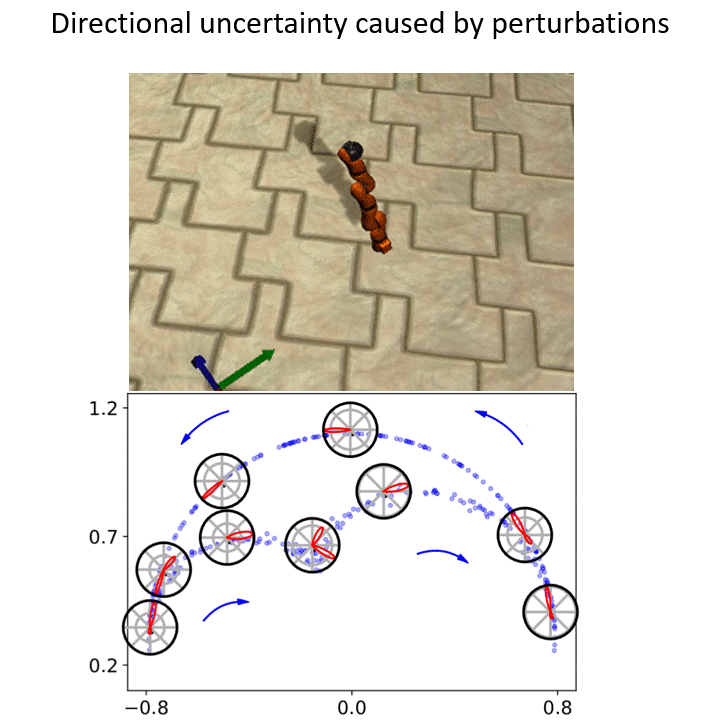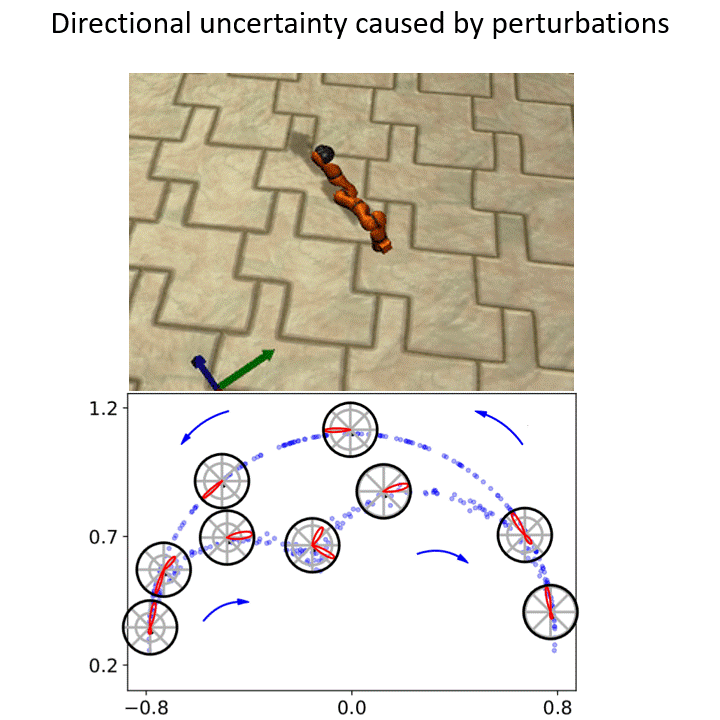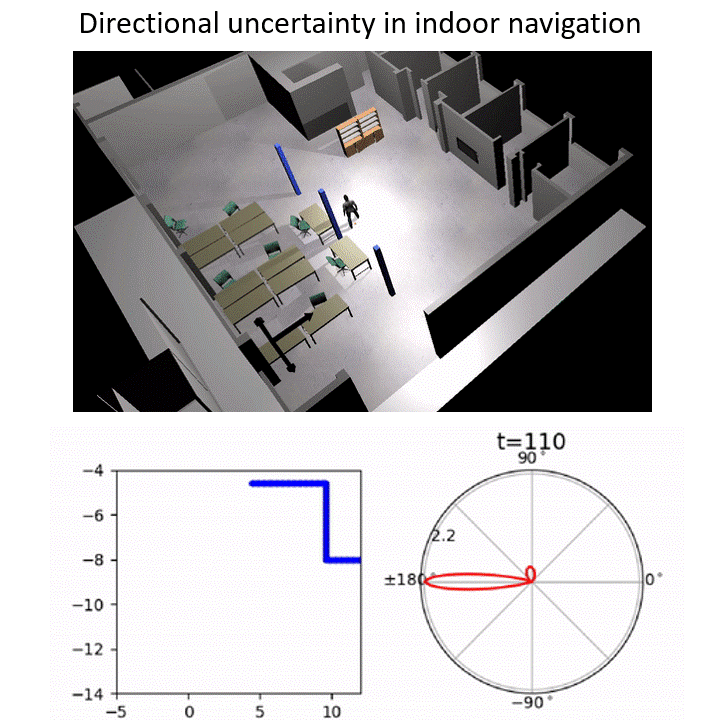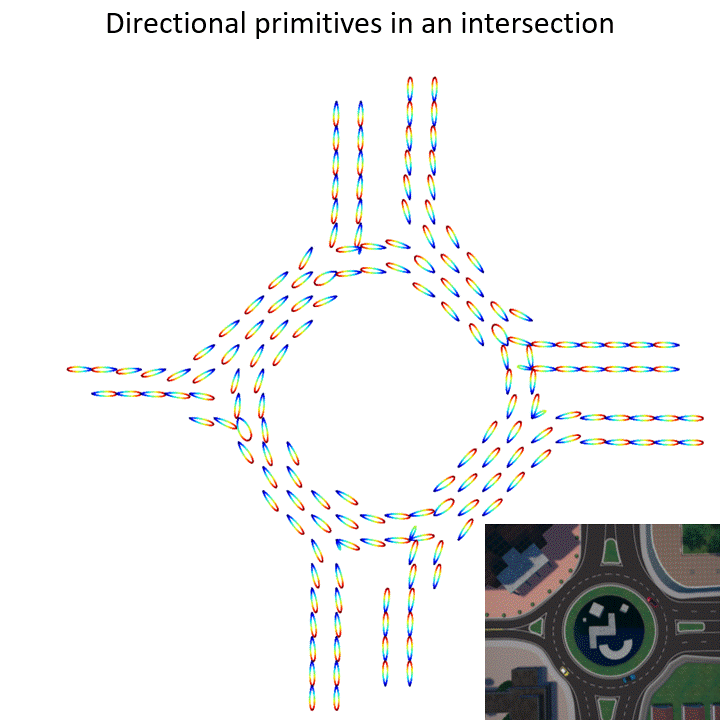
Estimating the directions of moving objects or flow is useful for many applications. I am mainly interested in modeling the multimodal aleatoric uncertainty associated with directions. Summary:
With the advancement of efficient and intelligent vehicles, future urban transportation systems will be filled with both autonomous and human-driven vehicles. Not only we will have driverless cars on roads but also we will have delivery drones and urban air mobility systems with vertical take-off and landing capability. How can we model the epistemic uncertainty associated with the velocity and acceleration of vehicles in 3D large-scale transportation systems?

Humans subconsciously predict how the space around them evolves to make reliable decisions. How can robots predict what would happen in the next few seconds around them? Summary:
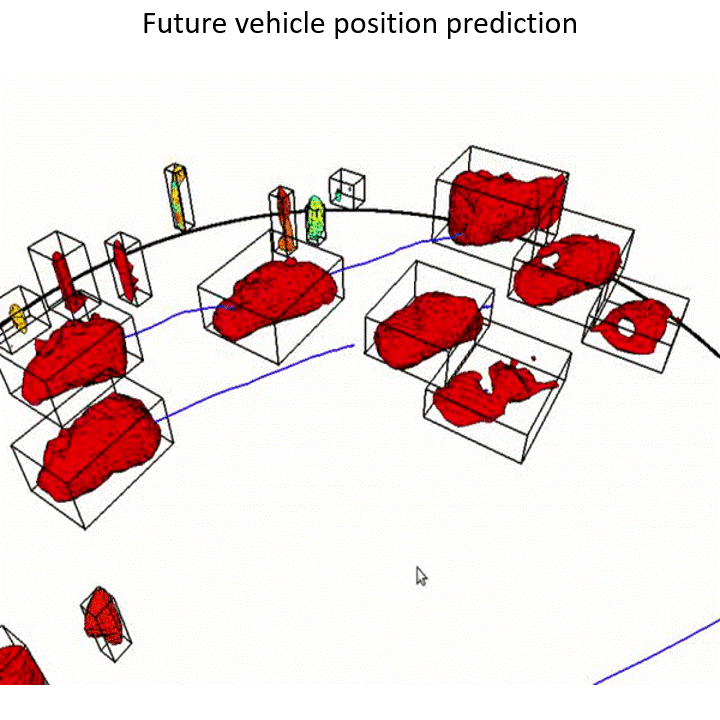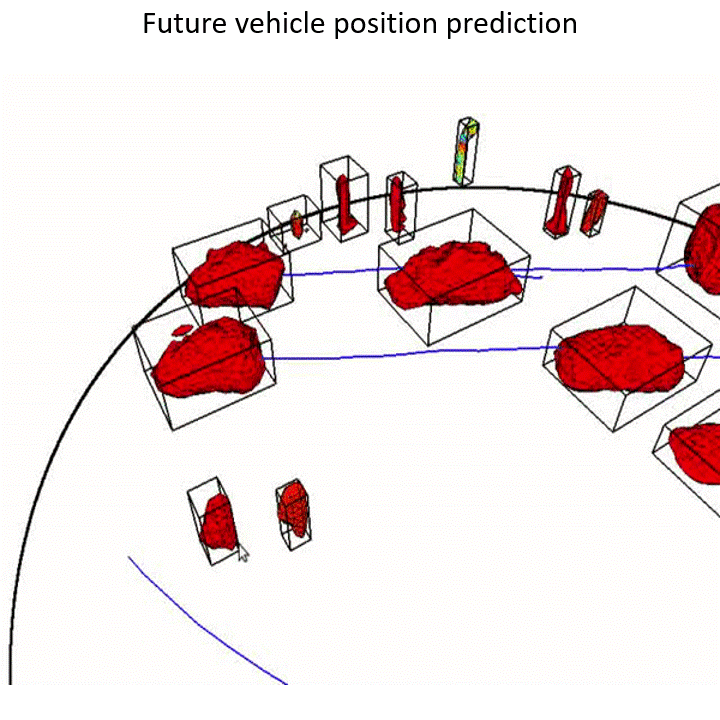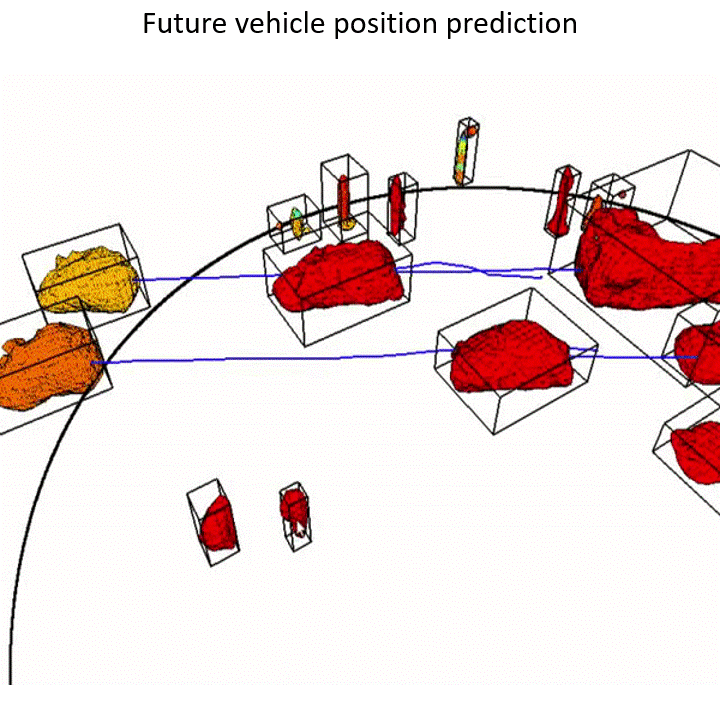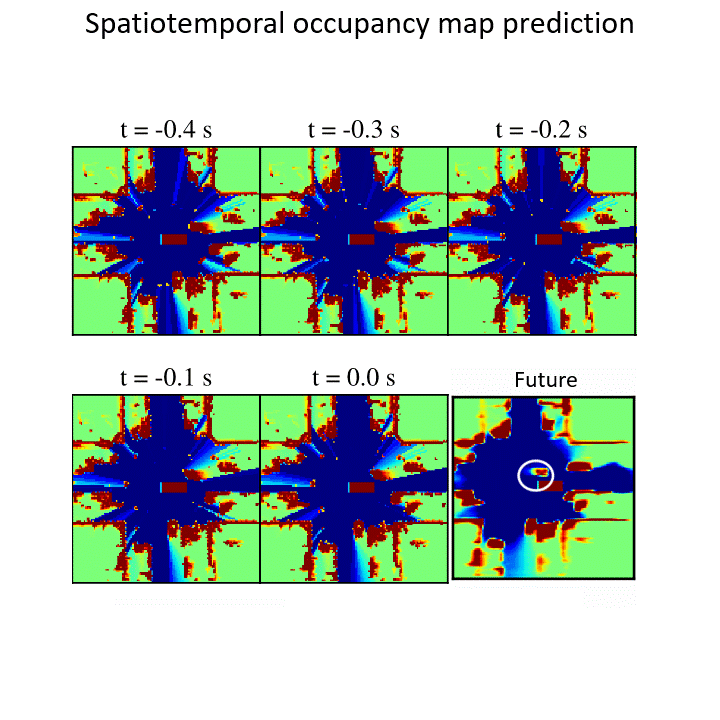
Summary:

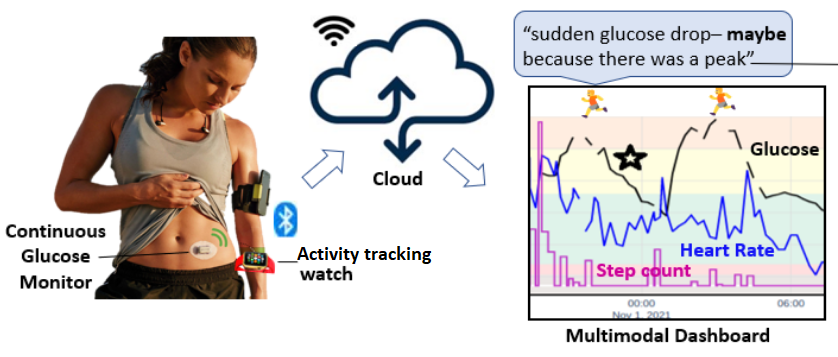
When humans operate in environments in which they have to follow some rules, as in driving, we cannot expect them to perfectly adhere to rules. Therefore, it is important to take into account this intrinsic stochasticity when making decisions. We specifically focus on developing uncertainty-aware intelligent driver models that are invaluable for planning in autonomous vehicles as well as validating their safety in simulation. Summary:

When robots operate in real-world environments, they do not have access to all the information they require to make safe decisions. Some information might even be partially observable or highly uncertain. How can agents account for this uncertainty? How can agents share information with each other to complete their individual tasks safely and efficiently? Summary:
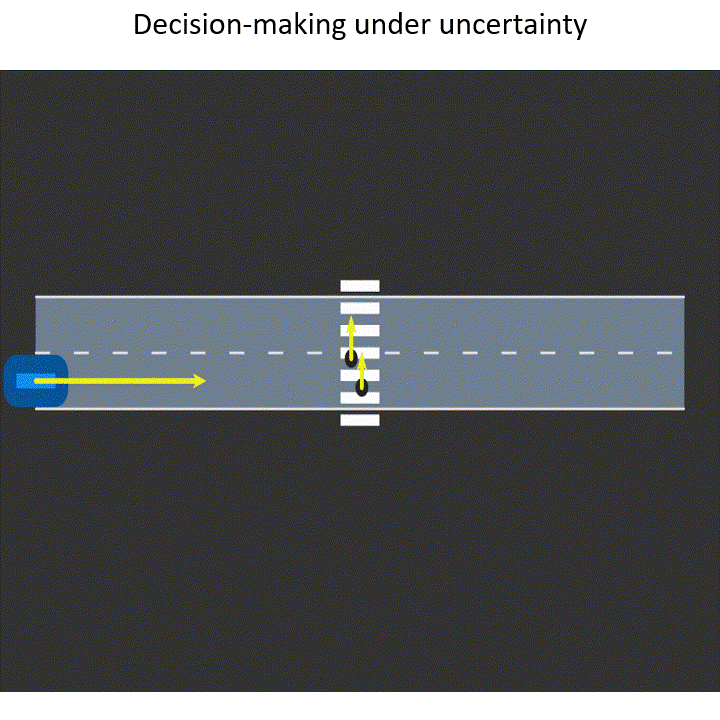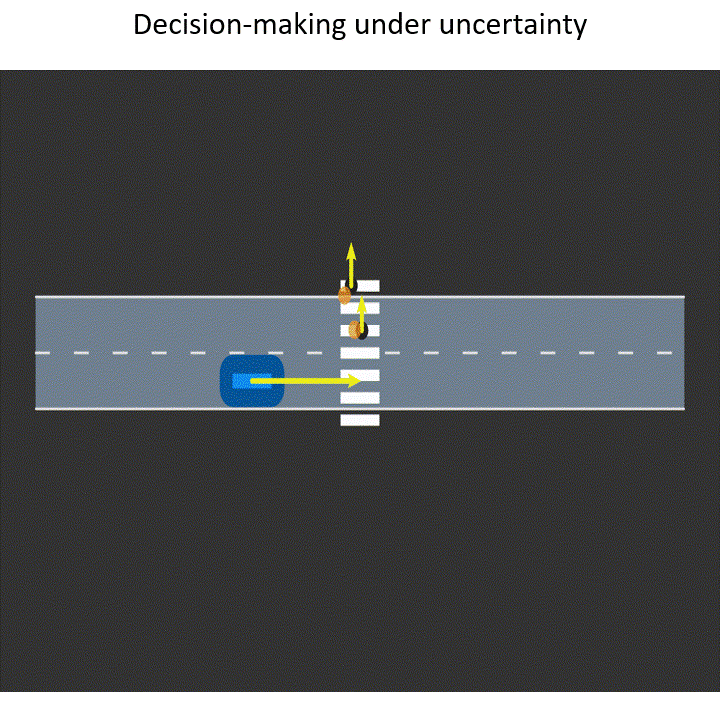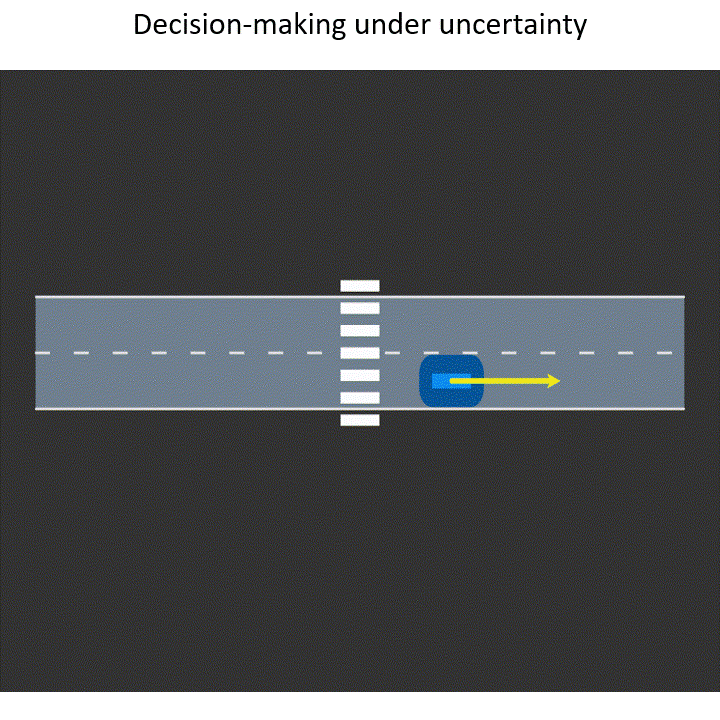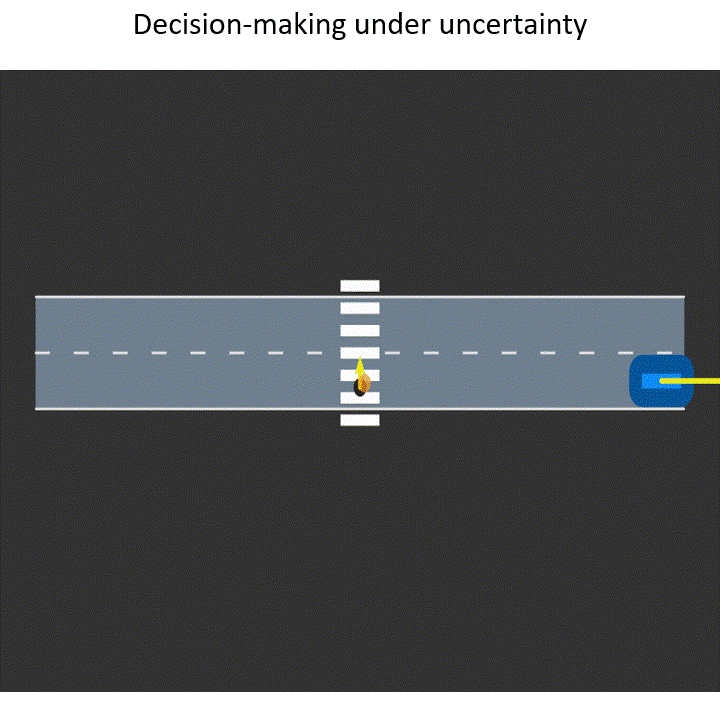
When a robot enters a new environment it needs to explore the environment and build a map for future use. Just think about what Romba does when we operate it in our home for the first time. Robots can also be used for gathering task-specific information such as search and rescue, subjected to constraints. Summary:
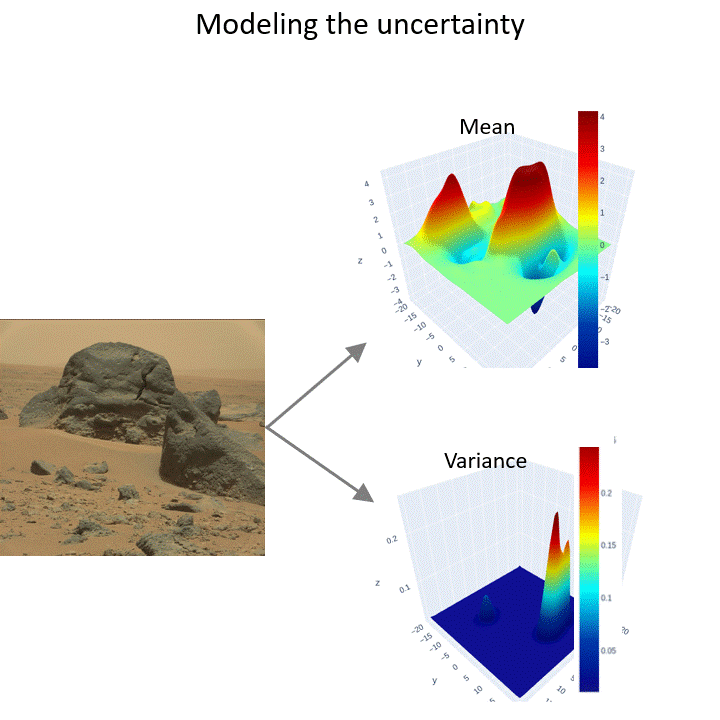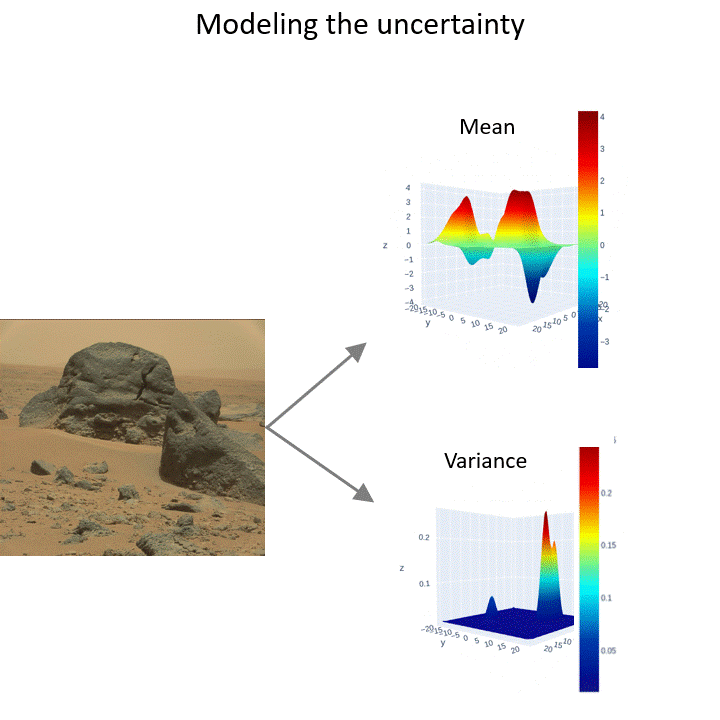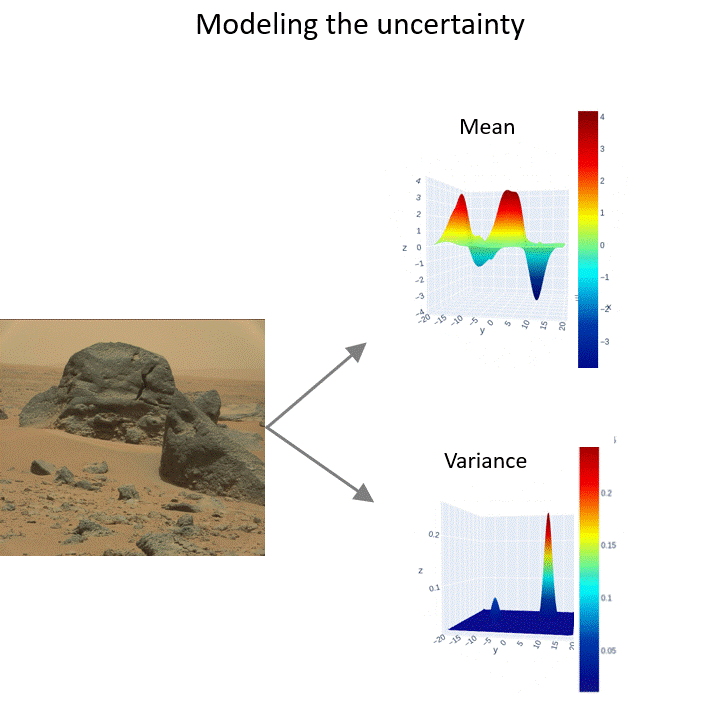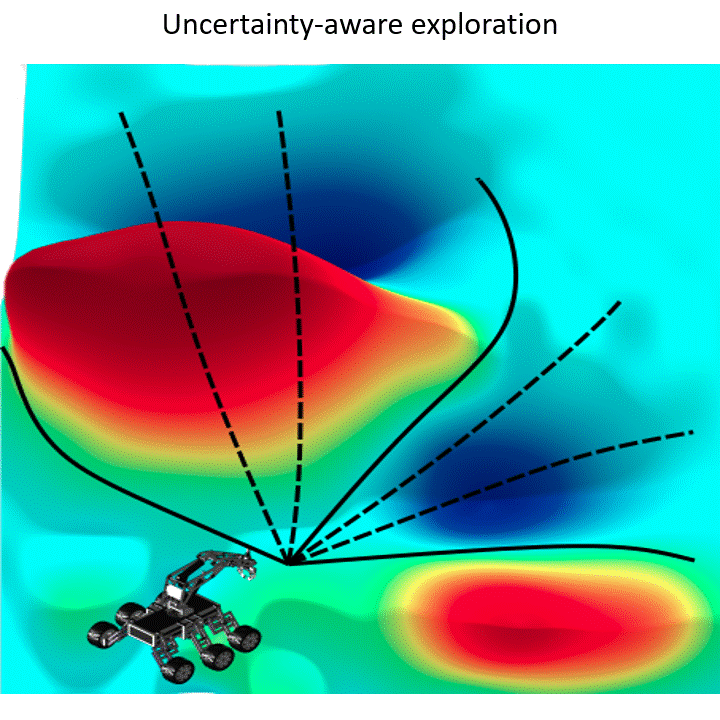

---